延续上节课的内容。
给定$|\cal H| = k$,给定$\delta, \gamma$,为了保证:
的概率不小于$1-\delta$,那么$m$需要满足:
假如$\cal H$是以$d$个实数为参数的(比如为了解决n个特征的分类问题,d就等于n+1),而在计算机中,实数多以 64 位浮点数保存,d 个实数就需要 64d 位来存储,那么$\cal H$的整个假设空间大小就为$2^{64d}$,也即$k=2^{64d}$,那么:
最直观的解释就是$m$与假设类的参数数量几乎是成正比的。
定义Shatter(分散):给定一个由$d$个点构成的集合:$S=\lbrace x^{(1)}, \ldots, x^{(d)} \rbrace$,我们说一个假设类$\cal H$能够分散(shatter)一个集合$S$,如果$\cal H$能够实现对$S$的任意一种标记方式,也即,对$S$的任意一种标记方式,我们都可以从$\cal H$中找到对应的假设来进行分割。
举例而言,如果${\cal H} = \lbrace \text{linear classification in 2D} \rbrace$(二维线性分类器的集合),对于二维平面上的三个点,有 8 种标记方式:
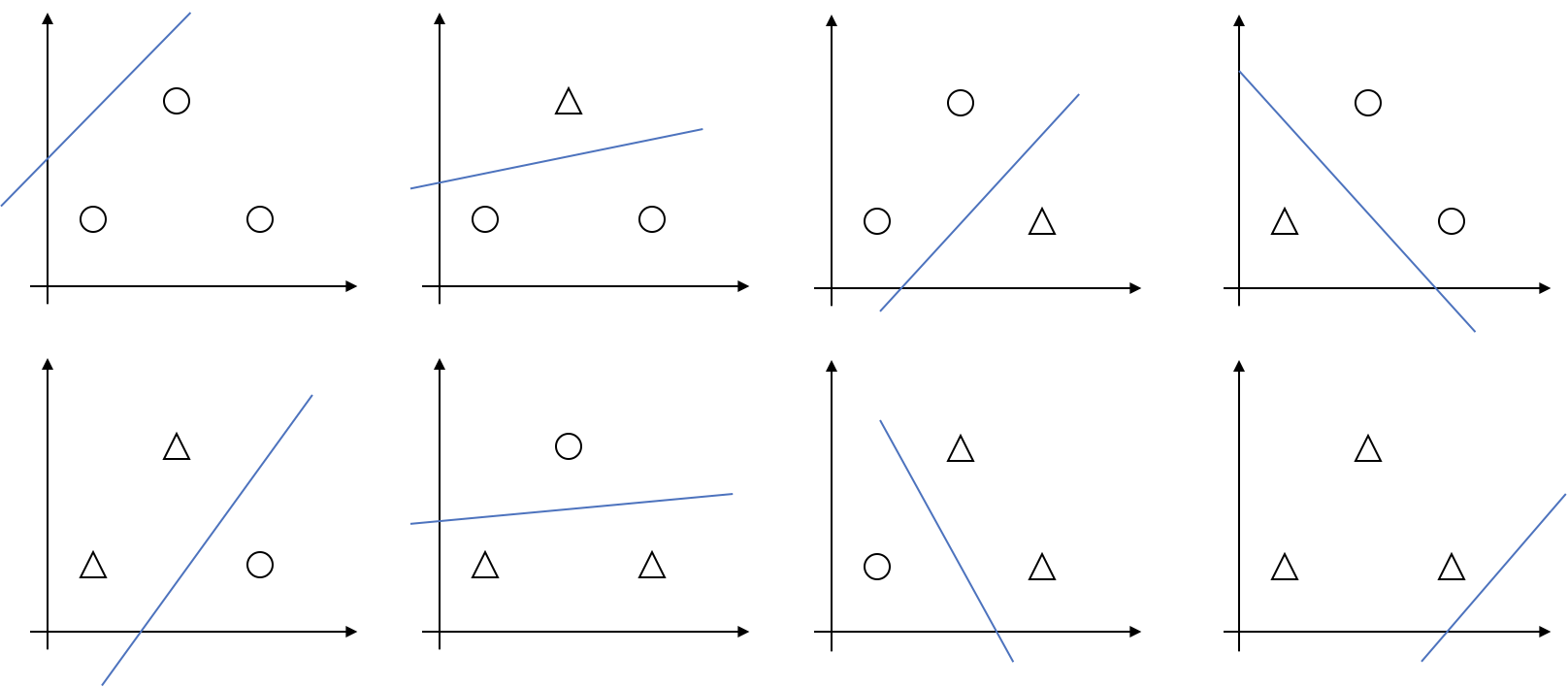
那么,蓝线所代表的线性分类器,都能完成对它们的标记,所以我们称$\cal H$能够分散平面上三个点所构成的集合。但是对于平面上四个点,就有存在以下这种情况,没有任何的线性分类器能够实现这种标记:
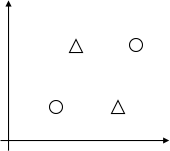
定义Vapnik-Chervonenkis dimension(VC 维):假设集$\cal H$的VC 维,写成$VC({\cal H})$,指的是能够被$\cal H$分散的最大集合的大小。
举例而言,如果$\cal H$是所有二维线性分类器构成的集合,那么$VC(\cal H) = 3$。当然并不是说$\cal H$要能分散所有三个点构成的集合,只要有某个三个点构成的集合能被$\cal H$分散即可,比如下面这种标记方式,$\cal H$就无法实现,但是我们还是称$VC(\cal H) = 3$。
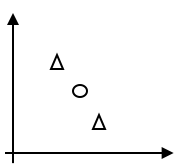
有一个推论:
$VC({\text{linear classification of n D}}) = n + 1$
定理:给定假设集合$\cal H$,令$VC({\cal H})=d$,那么,对于任意的$h \in {\cal H}$:
的概率不小于$1 - \delta$,以及
的概率不小于$1-\delta$。
引理:为了保证$\varepsilon({\hat h}) \leq \varepsilon(h ^ \ast) + 2 \gamma$至少在$1 - \delta$的概率下成立,应该满足:
$O_{\gamma, \delta}(d)$指的是,在固定$\gamma, \delta$的情况下,与$d$线性相关。
也即,$m$必须与$\cal H$的 VC 维保持一致,也可以这么理解,为了使泛化误差和训练误差近似,训练样本数目必须和模型的参数数量成正比。
在 SVM 中,给定数据集,如果我们只考虑半径 R 以内的点,以及间隔至少为$\gamma$的线性分类器构成的假设类,那么:
也就说明,$\cal H$ 的 VC 维上限,并不依赖于数据集中点$x$的维度,换句话说,虽然点可能位于无限维的空间中,但是如果只考虑那些具有较大函数间隔的分类器所组成的假设类,那么 VC 维就存在上界。
所以 SVM 会自动尝试找到一个具有较小 VC 维的假设类,所以它不会过拟合(模型参数不会过大)